Although it’s not possible to learn everything you need to know to quiz out of college trigonometry in 7 minutes, it is possible for you to understand the basics of trigonometry, sine, cosine, tangent, and theta, in just that short a time.
Yes, thanks to the power of the Mark Clarkson method, anyone can master a basic understanding of trigonometry in just 7 minutes. The first thing to know about trigonometry is that, despite its intimidating name, trigonometry is the study of right triangles. Period. That’s it. I swear. Right triangles. How do the parts of a right triangle relate to each other?
The second thing to know about trigonometry is that there are only two important numbers – sine and cosine. Everything else follows from sine and cosine. What are sine and cosine? The answer’s simpler than you might suspect.
Let’s say you take a small stick and poke it in the ground so it stands up on its own. You might want to measure the stick, and see how tall it is.

You notice that the stick casts a shadow on the ground. You measure the shadow to see how long it is.
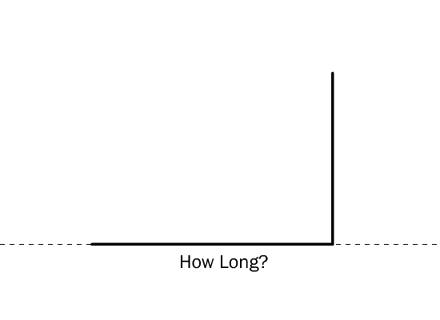
That’s your sine and cosine. Sine is how tall the stick is.
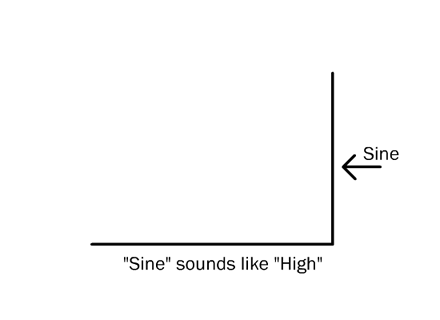
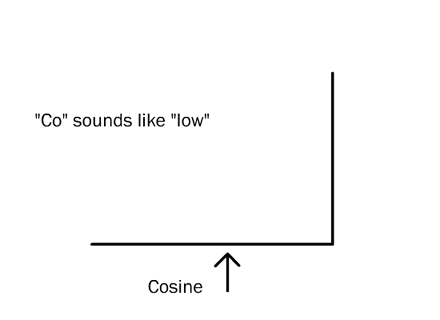
Cosine is how long the shadow is.Why are they called sine and cosine instead of, say, length and width? For arcane historical reasons and because it makes the uninitiated feel stupid. But that’s all they are. Here’s a mnemonic: sine and ‘high’ both have a long ‘i’ sound; ‘co’ and ‘low’ both have a long ‘o’ sound.
If you connect the open ends of your two lines (or your stick and its shadow), you’ll make a right triangle. As you remember, a right triangle is any triangle with a 90 degree angle in it somewhere, even if it faces left. Your stick and its shadow (the sine and cosine) are at right angles to each other, hence, a right triangle.
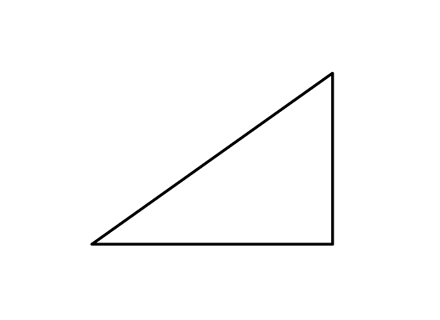
The line that closes the triangle is called the hypotenuse. I have no idea why.
The angle at the bottom left of the triangle is called ‘theta’. Theta is the only angle trig cares about.
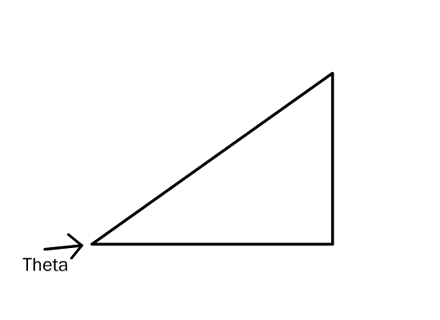
Theta derives from the sine and cosine. That is, if you know the sine and cosine, you can figure theta. Likewise, if you know theta, you can compute the sine and cosine. Every combination of sine and cosine results in a unique angle, theta (and vice versa). Put in a taller stick, or wait until the sun sinks lower in the sky, and theta changes.
Note: You can think about sine and cosine as arising from theta, or you can think about theta as arising from a particular sine and cosine, whichever you prefer. It doesn’t make any difference. Trig is about the relationship between these three numbers, sine, cosine, and theta.
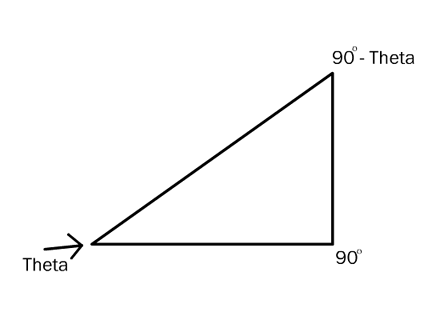
Since theta is the only angle trigonometry cares about, the other two angles don’t have a name. The one is always 90 degrees. The other is always 90 degrees minus theta.
Let’s say you measure the three sides of a triangle, and the measurements are 3, 4, and 5. It doesn’t matter 3,4, and 5 of what. Call it inches if that makes you more comfortable.
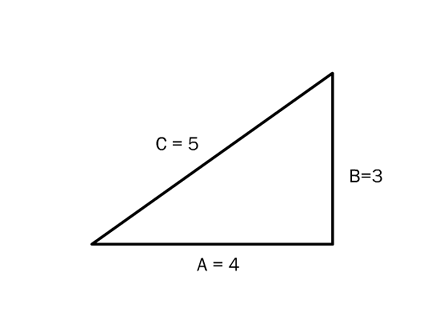
Now, you may remember that I said there were really only two numbers in trig. Here, however, you’ll notice that there are three numbers, A, B, C. That’s okay, because we’re going to throw one of those numbers — C, the hypotenuse — away. We don’t need it. Trig never uses it. How can that be? I’ll tell ya.
Those crafty Pythagoreans realized that they could simplify things considerably if they always assumed that the hypotenuse was equal to 1. Remember that: in trig, the hypotenuse is always equal to 1. Always.
But you measured your triangle and the hypotenuse wasn’t equal to 1; it was equal to 5. What to do? Simple, divide by 5 to make the hypotenuse equal to 1. Pretend that your triangle was 1/5th the size you measured.
If you divide all three sides by 5, the hypotenuse becomes 1; the sine becomes 0.6 (3/5); and the cosine becomes 0.8 (4/5).

If your hypotenuse had been 8, or 108,123, then you’d divide all your sides by 8, or by 108,123. If your measured hypotenuse had been 1/2, then you would have multiplied the sides by 2. Whatever it takes to make the hypotenuse equal one because, in trig, the hypotenuse is always 1.
You may have noticed that trigonometry is often applied to problems of circles and arcs and ellipses. Yet I insisted that it’s just about triangles, and only right triangles at that. Remember the old adage: “If your only tool is a hammer, then everything looks like a nail?” That applies to trigonometry very well. In trig, that hammer is the right triangle. Advanced trigonometry is about restating questions about circles and lines and curves and ellipses and whatever else mathematicians may think of, as questions about right triangles.
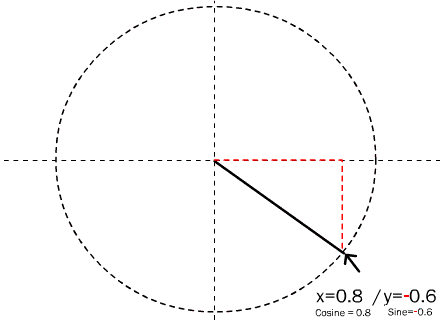
Let’s look at an example. Let’s superimpose our triangle onto a circle, so that the point of the angle, theta — the only angle we care about — falls on the origin, that is, the center point of the circle. Give this circle a radius of 1, the same as the hypotenuse of your triangle. The far end of the hypotenuse will just touch the perimeter of the circle. The X and Y coordinates of the point where the triangle touches the circle are 0.8 and 0.6 … your cosine and sine! Remember, cosine measures the length of the triangle, along the X axis. Sine measures the height of the triangle along the Y axis. So the cosine and sine correspond to the X,Y coordinates where the triangle touches the circle.
You can think about sine and cosine either as the coordinates of the point where the hypotenuse touches the circle, or as the lengths of the other two sides of the triangle, whichever seems more natural to you. It’s the same thing.

Look at the triangle above. Imagine that the hypotenuse, labeled ‘C’, is a hand on a clock. Right now it’s pointing to about 2 o’clock. As it moves toward 3 o’clock, imagine how the cosine, or ‘A’, will lengthen. Similarly, imagine how the sine, or ‘B’, will grow shorter.
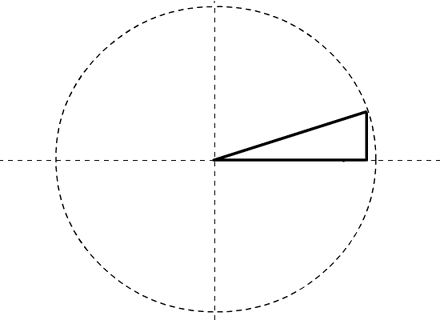
When the hypotenuse ‘hand’ reaches 3 o’clock, cosine will be 1, and sine will be 0. The triangle will have collapsed into a flat line.

As the hand continues to sweep around the clock, cosine will begin to shrink again, and sine to lengthen. (Notice that as the hand passes below 3 o’clock, the sine becomes negative; it’s now measuring the distance beneath the X axis.)
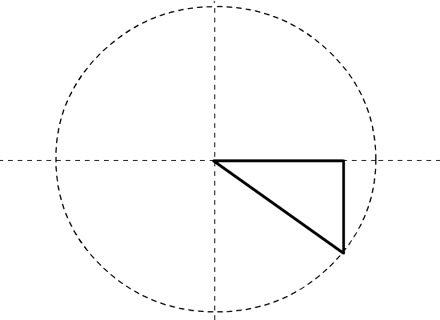
Both sine and cosine will alternate from 1 to 0 to -1 and back again. If you graph the sine (or cosine) over time, as the ‘hand’ sweeps around the ‘clock’, you’ll get – surprise! – a ‘sine curve.’
Start at the center of the circle and draw a straight line coming out from it at any angle, 0 to 360. The point where that line crosses the circle is the sine and cosine of that angle. The x coordinate of that point is the cosine of that angle. The y coordinate of that point is the sine of the angle.
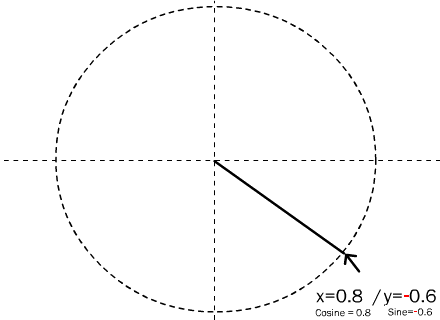
The right triangle may not always be shown, but it is always really there. It has to be, because trigonometry is only about right triangles.
Tangent
There’s another number that occurs almost as often as sine and cosine: tangent. The tangent is the slope of the hypotenuse. Whether we’re talking about roofs, or stairs, or right triangles, slope is rise over run. A roof which rises 3 feet for every 2 feet inwards has a steeper slope than a roof which rises 1 foot for every 2 feet inwards.
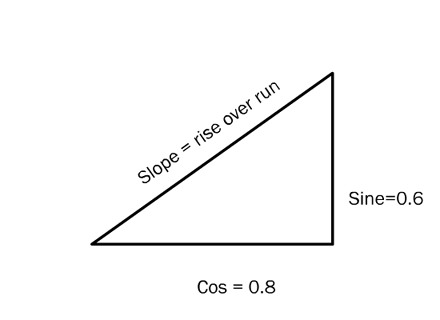
In the case of a right triangle, rise would be the same as sine. Remember, sine is the height of the triangle. The run would be the same as the cosine. Cosine is the length of the triangle.
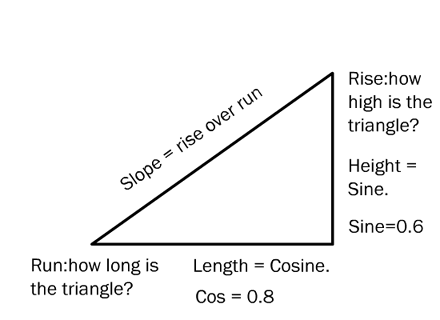
So the slope of the hypotenuse is defined by the sine (the rise) over the cosine (the run). In the case of your 3 by 4 by 5 triangle – or your 0.6 by 0.8 by 1 triangle, whichever – the tangent (or slope) would be 3 over 4 (3/4), or 0.75.
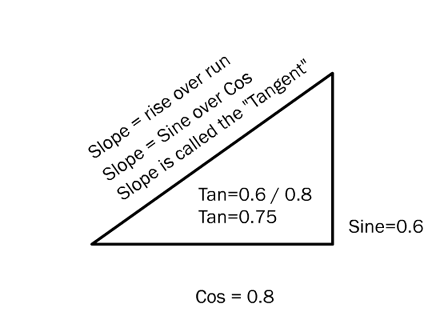
That’s it. That’s all there is. Everything else in trig is just increasingly abstruse ways of restating these relationships, and ways to restate different classes of problems as problems about right triangles.

love your 7 minute trig! hope you write a follow-up ie how to use these ratios to find theta or what is inverse cos?